Correlation vs Causal

Causality와 Probability의 Conditioning 부분이 너무 헛갈려서 애먹고 있는데, 몇몇 블로그¹²에서 아이디어를 얻고 연구실원의 도움을 받아 이해를 점점 하고 있는 중이다. 번역을 하면 나중에 까먹을 때 다시 돌아보기 좋겠지만, 그럴만한 시간은 없는 관계로 일단 intuition 정도만 정리를 해본다.

Conditional Probability

이번에 고민을 좀 하면서 확률에 대해서 다시금 생각해보게 되었다. 일반적으로 받아들여지는 확률의 연관성이라는 것이 인과성을 보장하지는 않는다. 따라서 우리가 흔히 하는 Classification이라는 Task에서도 어떤 패턴과 어떤 값 사이의 연관성이 있기 때문에 그것을 유추하는 것이지, 어떤 패턴이기 때문에 어떤 값이 도출된다라는 인과성은 아닌 것이다. 조건부 확률(Conditional Probability) \(p(A|B)\) 라는 것도 어떤 값 \(B\)가 주어졌을 때, 다른 값 \(A\)가 함께 나타날 확률이라는 것은 연관성(Likelihood)이지 인과성은 아닌 것이다. \(B\)가 나타났기 때문에 \(A\)가 나타난 것은 아니다. 그냥 데이터를 보니(seeing) 하필이면 그러한 패턴=연관성=관계가 나타났을 뿐이다. 그리고 앞으로도 그러한 패턴이 나올 확률이 높기 때문에 우리는 그러한 결론은 도출해낸다. 하지만 데이터에서 하필이면 그런 연관성이 왜 나왔는지는 알 수가 없다.

그림출처 ¹

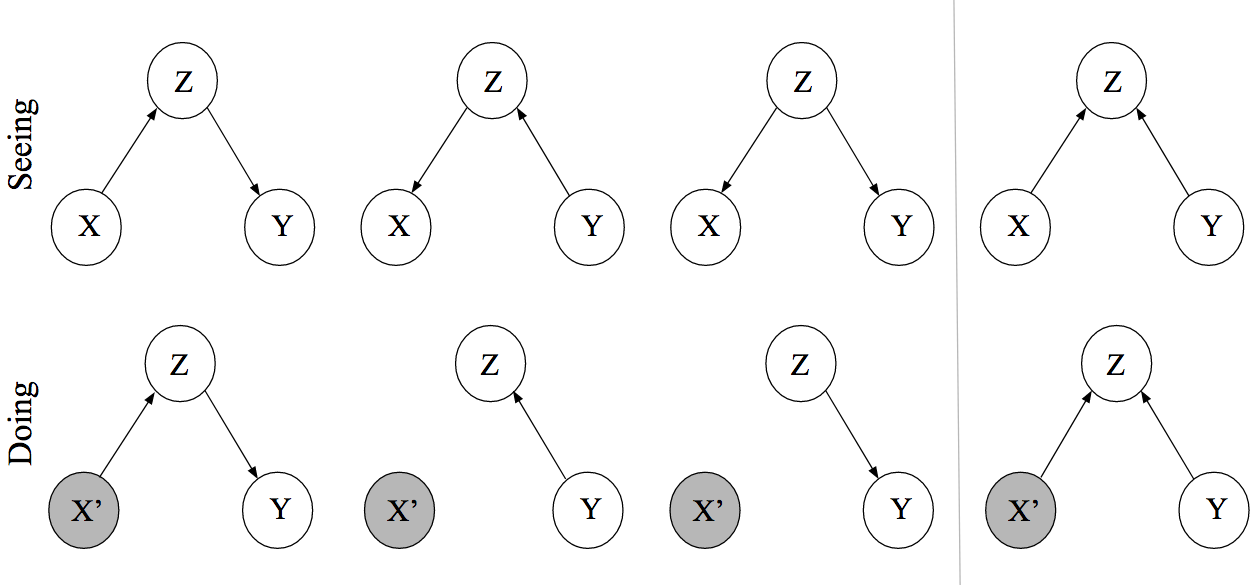
Seeing

흔히 생각하는 베이지안 네트워크를 떠올려야 한다. 여기서의 DAG는 “연관성(Association)”에 관련된 것이다. 예를 들어 위쪽 열의 첫번째 그림 \(p(X, Y, Z) = p(Y|Z)p(Z|X)\) 은, \(Z\)는 \(X\)에 영향을 받아 연관성을 가지게 된다. 만약 우리가 \(Z\)를 관찰(observe)할 수 없다면, \(p(Y|X)\)는 어떤 연관성을 가지는 것 처럼 보일 것이다. 예컨대 양의 관계라고 한다면 \(Y\)가 증가하면 \(X\)도 증가하는 것처럼. 그러나 \(Z\)를 관찰하는 순간 더 이상 직접적인 관계는 사라진다. 왜냐하면 \(X\)와 \(Y\)의 관계(연관성)를 결정짓던 요인은 사실 \(Z\)이므로 이것만 알게되면 \(X\)와 \(Y\)가 \(Z\)에 의해 관계를 맺는다라고 말할 수 밖에 없기 때문이다.

이러한 점에서 바라보면 위쪽 열의 세 그림가장 오른쪽 그림 제외)은 실제 데이터 관측에서는 구별을 해낼 수 없다. 결과적으로 우리가 구하게 관찰하게 되는 값은 \(X, Y\)일테고 (혹은 \(Z\)를 관찰가능하거나 잠재 변수라고 생각할지라도) 그 두 변수가 연관성이 있는 방향으로 관찰이 된다라는 것 이상으로는 무언가를 판단하기 힘들다.

Doing

우리는 어떠한 변수가 특정 값을 가졌을 때 어떤 변화가 생기는지 그 인과 관계를 알고 싶다. 기존의 Seeing에서는 연관성만 알 뿐 이었고, 인과성을 모르는 이유는 결국 \(X, Y\)에서 연관성=패턴=관계를 만들어내게 하는 요인이 있을테지만 우리는 그것을 모른다라는 점 때문이다. 하지만 만약에 우리가 어느 정도의 도메인 지식들로 하여금 \(X, Y\)에 대해 동시에 영향을 미칠 수 있는 조건 \(Z\)를 알고선 DAG를 만들어 본다면 위와 같은 모양들 중 하나(아래열, 왼쪽에서 세번째)로 나타날 것이다.

Doing에서는 Causal Graph라는 것으로 이해를 해야한다. Causal Graph란 각 노드의 부모 노드는 직접적인 인과성(Direct Causes)을 포함하는 베이지안 네트워크를 말한다.³ 따라서 Seeing의 베이지안 네트워크보다 좀 더 speicific한 네트워크를 가진다고 할 수 있겠다. 또, 직접적인 인과성(Direct Causes)라는 것은 자식 노드에 연결되어 있는 모든 부모들 중에 하나의 부모 노드만 다른 값으로 변화시키는 경우 자식 노드의 확률 분포의 변화를 야기시킬 수 있다는 것을 의미한다.예컨대 가장 오른편의 그림에서 직접적인 인과성을 본다면 부모 노드 중 하나인 \(Y\)만을 바꾸어주었을 때 자식 노드인 \(Z\)의 확률 분포는 변화하게 된다. 즉, \(p(Z=z|X=x, Y=y) \neq p(Z=z|X=x, Y=y') = p_{do(Y=y')}(Z=z|X=x)\)

여기서 중요하게 넘어가야할 점은 개입(Intervention)이라는 개념이다. 만약 \(X\)에 특정값으로 개입을 한다고 생각해보자. 아래열 두번째 그림에서 \(Z\)는 변수 \(X\)에 인과성을 지니는 부모 노드이다. 그러나 \(X\)가 특정값으로 개입되어 고정이 된 상태라면 더 이상 인과성은 없어지게 된다. \(Z\)를 아무리 변화해도 \(X\)는 실험자가 개입한 상태에서 변화가 없기 때문이다. 세번째 그림도 마찬가지인 상황이므로 똑같은 그래프로 남게 된다. 우리는 우리가 개입하고자 하는 노드에서 들어오는 방향의 화살표를 제거해주는 것으로 Causal Graph를 수정해줄 수 있게 된다.

이러한 과정은 \(X\)와 \(Y\) 사이에서 특정한 인과성을 보고자 할 때, 기존의 연관성만 볼 수 있는 Seeing 단계 혹은 Observational Study에서는 \(Z\)라는 변수가 항상 존재하기 때문에 우리는 \(X, Y\)를 직접적으로 비교해볼 여유가 없다. 그러나 인과성을 끊어주는 순간 우리는 오롯이 \(X\)의 값으로만 \(Y\)의 변화를 판단할 수 있게 된다 (\(Z\)는 우리가 흔히 하듯이 Marginalized out/Weighted sum을 하면 되고 이것은 \(Y\)에게만 영향을 미칠 뿐 \(X\)의 값에 대해서는 하등 상관이 없게되겠다).

Counterfactual

이 부분은 조금 더 공부를 해야될 것 같다.

Reference

1. https://fabiandablander.com/r/Causal-Inference.html ↩ ↩²

2. https://www.inference.vc/causal-inference-2-illustrating-interventions-in-a-toy-example/ ↩

3. http://www.homepages.ucl.ac.uk/~ucgtrbd/talks/bayesnetmeetup_causality.pdf ↩